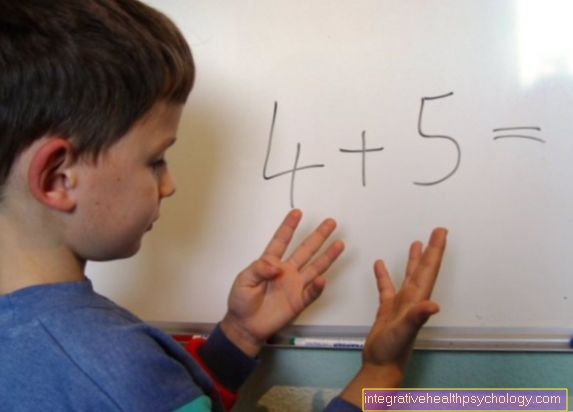Симптоми слабкості в численності
Синоніми в більш широкому значенні
Особливості, симптоми, аномалії, раннє попередження, арифметична слабкість, арифмастенія, акалькулія, порушення навчання математиці, труднощі в навчанні на уроках математики, порушення арифметики, порушення часткової продуктивності, дискалькулія, дислексія, слабкість читання та орфографії, ЛРС.
раннє виявлення
Щоб можна було визначити відхилення від норми, необхідно знати, що насправді називається нормою. Що стосується арифметичних слабкостей (але також і будь-якої іншої проблеми навчання, наприклад, слабких читання та написання), це означає, що ви спочатку дізнаєтесь, яких стандартів слід досягти, коли і де.
Визначити це у шкільній сфері не є особливо складним через визначені навчальні цілі та стандарти, яких слід досягти, яких необхідно досягати конкретно в кожному навчальному році.
А як щодо відхилень у роботі дошкільного закладу?
Чи є тут якісь ознаки, які говорять про те, що проблеми з навчанням ймовірні?
Якщо так: Що можна зробити діагностично та терапевтично, щоб ймовірність інвалідності у навчанні була максимально низькою?
Проблеми розвитку в дитячому садку
Основна ідея дитячого садка походить від Фрідріха Фребеля, який у 1840 р. Наповнив свою основну ідею змістом і перетворив її на реальність. Він мав бачення місця для дітей, яке приймало та підтримувало всіх дітей незалежно від їх соціального походження та ґрунтувалося на принципі розширеної сім'ї. У центрі уваги завжди було грати разом, соціальну взаємодію та доглядати за дитиною. Дитячий садок також повинен бути місцем контактів між сім’ями та заохочувати до взаємодії.
Дитячий садок та основна ідея Фробеля підлягали - як і інші освітні райони - різному впливу. Педагогічні концепції були змінені та адаптовані до соціальних умов та змін. Політичні впливи можна також довести, якщо їх шукати.
Внаслідок змінених умов життя, особливо через змінене дитинство, дитячий садок чи дитячий садок набувають все більшого значення як важливий заклад опіки маленьких дітей.
Як і в контексті Раннє виявлення слабких сторін числення звернувшись, формуються основи Вимоги як: Сприйняття - зберігання - рухові навички та уява після того, як основний камінь був закладений в утробу матері завдяки взаємодії з навколишнім середовищем у малюка і, таким чином, у дошкільному віці. Вони впливають на навчання особливим чином і часто несуть спільну відповідальність за розвиток проблем у навчанні (погана чисельність, погана концентрація, погане читання та написання, ...). Ці компоненти можна просувати за допомогою різних вправ.
Дитячий садок, який у своїй ідеальній формі інтегрує освіту, догляд та виховання один з одним, може мати фундаментальний вплив. Власні переживання дитини є найважливішою основою безкоштовно згідно з висловом Конфуція:
Скажи мені, і я забуду!
Покажіть мені, і я згадаю!
Дозвольте мені це зробити і я зрозумію!
Проблеми з розвитком вже можна знайти в дошкільній зоні. Однак тут рекомендується обережність, адже не кожне відхилення від норми означає, що проблеми в навчанні в шкільному секторі обов'язково будуть розвиватися. Однак "здорова" пильність не може зашкодити. Вирішення проблем, коли ви їх помічаєте, не приносить ніякої шкоди, якщо це не призведе до надмірного акціонізму. У будь-якому випадку слід запобігати, щоб відхилення були «надмірно оброблені». Наприклад, якщо ви виявите ненормальність у зоровому сприйнятті дитини, цю здатність не слід навчати цілодобово. Потім його слід інтегрувати насамперед у грайливе протистояння дитини і час від часу слід перевіряти успіх дитини.
Деякі серйозні порушення можуть потребувати консультації з педіатром. Як дошкільний заклад, ваш дитячий садок може надати вам додаткову інформацію щодо цього.
Наступний список присвоює основні можливості різним відхиленням. Вона не претендує на повну. Віднесення аномалій до здібностей не завжди зрозуміло. Іноді є кілька основних навичок, саме тому відхилення згадуються двічі.
Наступні проблеми не обмежуються також дошкільною територією. Вони, безумовно, можуть існувати ще в шкільному віці. Єдине правило тут: Якщо виникають відхилення: будьте пильні!
Наступні відхилення можуть вказувати на проблеми з навчанням:
сприйняття:
- Проблеми із торканням предметів під зав'язаними очима.
- Проблеми з називанням частин тіла, які торкалися із закритими очима.
- Проблеми із вислуховуванням певних звуків та / або комбінацій звуків
- Пальчива агнозія (неможливість розрізнити певні пальці на руці та показати їх за запитом)
- Проблеми з візуальним виявленням менших кількостей до кількох шести предметів (наприклад, точки куба зображення; Кавальне каміння, яке вийшло з ладу; поворотні плити, каміння ...); Кількість треба рахувати!
- З цим пов'язані також: Проблеми з придбанням відносин: більше / менше; більше / менше ніж; однакова кількість, ....
- Проблеми в області поєднання певних областей сприйняття, напр. Проблеми з рукою - очима - координація (торкання певних предметів)
- Проблеми з фарбуванням (перетинання ліній)
- Проблеми з сортуванням елементів за певними критеріями.
- Проблеми, що імітують ритми (плескаючи, ...)
- Проблеми в області просторової орієнтації
зберігання:
- Проблеми з іменуванням предметів, які ви бачили раніше, але потім вилучені або охоплені.
- Проблеми з додаванням рядків (червоне коло, синій трикутник, зелений квадрат, жовтий прямокутник, ...) або з реконструкцією фігур з пам'яті.
- Проблеми запам'ятовування
- Проблеми з повторенням слів, складів та чисел, але також: Проблеми, що повторюють безглузді слова / склади, але також повторюють рядки чисел.
Моторні навички:
- Проблеми в області грубої рухової майстерності (при бігу, присіданні, ловінні, балансуванні, ...)
- Проблеми з дрібною моторикою (фарбування, тримання ручки, ігри з пальцями, зав'язування взуття, ...)
- Проблеми з плесканням або плесканням у заданих ритмах
- Проблеми, що імітують рухи / послідовності рухів.
- Проблеми, що імітують жести та / або міміку.
- Проблеми при перетині середньої лінії (наприклад, коли діти повинні робити поперечні рухи, наприклад, рухатися вперед / назад або вбік, правою рукою торкатися лівого коліна або навпаки
ідея:
- Проблеми з переказом історій через брак уяви (створення образів в голові)
- Проблеми з продовженням логічного ряду
- Проблеми з фарбуванням (перетинання ліній)
- Проблеми з планувальною діяльністю (визначення порядку: спочатку ..., потім ...)
початкова школа
Принцип самодіяльності, безумовно, також повинен бути закріплений як важливий елемент у початковій школі.
Визнання недоліків у розрахунку вимагає розширення перспективи. Важливим є не лише той факт, чи правильно було розраховано завдання, але й шлях, який пройшов для вирішення задачі. Правильні рішення не обов'язково говорять про дитячу грамотність та вміння. Особливо в перші роки школи учні можуть розраховувати до своєї мети. Не можна недооцінювати здатність дітей з поганою працездатністю приховувати свої проблеми.
Розвиток математичного мислення знаходиться в центрі складних досліджень. Піаже провів дослідження з цього приводу в 1960-х роках і виявив, що розвиток поняття числа багато в чому залежить від здатності візуально - просторової уяви.
Розробка поняття чисел, поетапне розширення діапазону чисел до мільйона (на четвертому році школи) та поступове проникнення таких же є в центрі уваги уроків математики в початковій школі.
Розробка діапазонів чисел відбувається поетапно, можна робити підрозділи та здійснювати переходи вільно в кінці навчального року. Наприклад, діапазон чисел можна збільшити до 100 наприкінці першого року навчання в школі. Потім математичне проникнення діапазону чисел відбувається в другому навчальному році.
Діапазон чисел до 20
Області навчання:
- Риси та стосунки
- Числа - додавання і віднімання
- Розміри
- геометрія
Діапазон чисел до 100
Області навчання:
- Розширення діапазону чисел
- Додавання і віднімання
- Множення та ділення
- Властивості чисел / наборів чисел
- Розміри
- геометрія
Діапазон чисел до 1000
Області навчання:
- Розширення діапазону чисел
- Додавання та віднімання / письмові методи обчислення
- Множення та ділення
- Властивості чисел / наборів чисел
- Розміри
- геометрія
Діапазон чисел до 1 000 000
Області навчання:
- Розширення діапазону чисел
- Додавання і віднімання
- Методи множення та ділення / письмові обчислення
- Властивості чисел / наборів чисел
- Розміри
- геометрія
Розробка концепції чисел та орієнтації в просторі чисел надається особливого значення, оскільки проникнення та здатність орієнтуватися у відповідному просторі чисел має особливе значення для всіх інших областей відповідальності. Що також включає:
- згрупування для побудови системи цінностей декадальних місць,
- робота з дошкою цінностей
- орієнтація на рядку чисел, смузі чисел, табло, поля сотень / тисяч, ... для створення числових зв’язків (наступник, попередник, сусідні десятки, сотні, тисячі, ...
- написання та читання чисел (числові диктанти, ...)
- Порівняйте та впорядкуйте (відносини: ... менше, ніж ..., ... більше, ніж ..., ...
- різний аспект числа (номер картки (число), порядковий номер (послідовність: перший, другий, ...), міра (число у зв'язку з кількістю), номер оператора (номер у зв'язку з командою обчислення), ...)
- структура властивостей чисел (парне / непарне; ділиться / не ділиться; ...
- Округлення чисел
- ...
1 клас
Навіть у зоні дошкільного віку діти мають різноманітний досвід з кількістю, кількістю та розмірами, а також з простором та часом. Ці знання та вміння використовуються та розвиваються на початкових уроках.
На уроках математики на першому курсі школи також вводиться правильне написання цифр і, крім переймання та розвитку різних попередніх досвіду, вводяться перші операції (додавання та віднімання). Для того щоб отримати уявлення про математичні операції, операції спочатку вводяться на рівні дії. Додавання - це не що інше, як доповнення (збільшити, додати, заповнити, ...), віднімання представлено видаленням (зменшенням, скороченням, ...).
Більшості дітей легко перейти на символічний рівень через розуміння та різноманітні вправи, але є також відхилення та відхилення, які показані нижче.
Риси та стосунки
- Проблеми з паруванням.
- Проблеми з визначенням кількості (скільки 6 ведмедів?)
- Проблеми перевірки перцептивної відповідності елементів двох множин
- Проблеми при завершенні відносин (... менше, ніж ..., ... більше, ніж ..., рівні)
Віднімання додавання чисел
- Ротатор чисел (12 замість 21) під час читання та запису.
Обертові цифри також можуть символізувати проблеми при захопленні значення місця. - Просторова нестабільність: 9 і 6 змінюються місцями, цифри (особливо 3 або 1) записуються неправильно навпаки (аналогії з просторовою нестабільністю у випадку слабкості читання та написання)
- Проблеми з підрахунком, особливо підрахунком
- Проблеми з визначенням попередника та наступника (орієнтація в просторі чисел)
- Проблеми з розумінням додавання та / або віднімання
- Проблеми розв’язування задачі, розворот завдання та / або додаткове завдання
- Проблеми при перевищенні десятків (запам'ятовуючи проміжні результати)
Розміри
- Проблеми із захопленням кількості
- Проблеми з вступом у відносини (наприклад, при розрахунку з грошима: 3 євро> 4 центи.
геометрія
- Проблеми з іменуванням функцій
- Проблеми з ідентифікацією квадрата, прямокутника, трикутника, кола.
- Проблеми з дотиком та сортуванням за певними критеріями.
2 клас
Розширення діапазону чисел:
- Проблеми в розумінні системи цінностей місць P
- Проблеми з читанням чисел
- Проблеми із записом чисел на слух
Додавання і віднімання:
- Розрахунок пальцями зберігається
- Невеликі завдання плюс (завдання додавання та віднімання в ЗР до 20) ще не автоматизовані
- Додавання та віднімання здійснюються лише за допомогою підрахунку (також на сто таблиці)
- Проблеми зі схемами розрахунків будівель. (Додайте до наступних десяти, а потім продовжуйте: ПЕРШИЙ ..., ТАК)
- Проблеми з фактичною арифметикою, які не зумовлені недоліками / слабкостями у змістовному читанні
- Проблеми в розумінні завдань, розвороту та доповнення
- Проблеми з перерахуванням переказів
Множення та ділення:
- Проблеми з навчанням та автоматизацією таблиць множення
- Проблеми з відображенням множення як множинного додавання
- Проблеми в розумінні завдань, розвороту та доповнення
Властивості чисел і набори чисел:
- Проблеми з розумінням системи цінностей місць
- Проблеми з читанням чисел
- Проблеми із записом чисел на слух
Розміри:
- Проблеми з введенням розмірів
- Проблеми із захопленням кількості
3 клас
Розширення діапазону чисел:
- Проблеми з розумінням системи цінностей місць.
- Проблеми з читанням чисел
- Проблеми із записом чисел на слух.
Додавання і віднімання:
- Розрахунок пальцями зберігається.
- Невеликі завдання плюс (завдання додавання та віднімання в ЗР до 20) ще не автоматизовані.
- Додавання та віднімання здійснюються лише за допомогою підрахунку.
- Проблеми в розумінні завдань, розвороту та доповнення
- Проблеми зі складанням письмового доповнення
- Проблеми з виконанням (додаткові завдання), а отже, і проблеми з налаштуванням письмового віднімання
- Проблеми з письмовим відніманням кількох мінусів (= числа, які слід відняти від числа)
- Проблеми із збереженням проміжних результатів
- Проблеми з фактичною арифметикою, які не зумовлені недоліками / слабкостями у змістовному читанні
- Проблеми з перерахуванням переказів
Множення та ділення:
- Проблеми з навчанням та автоматизацією таблиць множення.
- Проблеми з відображенням множення як множинного додавання.
- Проблеми в розумінні завдань, розвороту та доповнення
Властивості чисел і наборів чисел:
- Проблеми з розумінням системи цінностей місць.
- Проблеми з читанням чисел
- Проблеми із записом чисел на слух.
Розміри:
- Проблеми з введенням розмірів
- Проблеми із захопленням кількості
4 клас
Розширення діапазону чисел:
- Проблеми з розумінням системи цінностей місць.
- Проблеми з читанням чисел
- Проблеми із записом чисел на слух.
Додавання і віднімання:
- Розрахунок пальцями зберігається.
- Невеликі завдання плюс (завдання додавання та віднімання в ЗР до 20) ще не автоматизовані.
- Додавання та віднімання здійснюються лише за допомогою підрахунку.
- Проблеми в розумінні завдань, розвороту та доповнення
- Проблеми зі складанням письмового доповнення
- Проблеми з виконанням (додаткові завдання), а отже, і проблеми з налаштуванням письмового віднімання
- Проблеми з письмовим відніманням кількох мінусів (= числа, які слід відняти від числа)
- Проблеми із збереженням проміжних результатів
- Проблеми з фактичною арифметикою, які не зумовлені недоліками / слабкостями у змістовному читанні
- Проблеми з перерахуванням переказів
Множення та ділення:
- Проблеми з навчанням та автоматизацією таблиць множення.
- Проблеми з відображенням множення як множинного додавання.
- Проблеми в розумінні завдань, розвороту та доповнення
Властивості чисел і наборів чисел:
- Проблеми з розумінням системи цінностей місць.
- Проблеми з читанням чисел
- Проблеми із записом чисел на слух.
Розміри:
- Проблеми з введенням розмірів
- Проблеми із захопленням кількості















.jpg)